সাইন নিয়ম

পদার্থবিজ্ঞানের সাইন নিয়মের জন্য স্নেলের সূত্র দেখুন।

ত্রিকোণমিতিতে সাইন নিয়ম বা সাইনের সূত্র (ইংরেজি: Sine rule) বলতে একটি সমীকরণকে বোঝায় যা কোনো ত্রিভুজের তিনটি বাহু ও তাদের প্রতিটির বিপরীত কোণের সাথে সম্পর্ককে চিহ্নিত করে।

ত্রিভুজের তিনটি বাহু ও তাদের বিপরীত কোণ

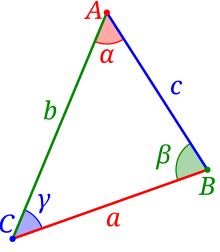
$${\frac {a}{\sin {\alpha }}}\,=\,{\frac {b}{\sin {\beta }}}\,=\,{\frac {c}{\sin {\gamma }}}\,=\,2R$$ যেখানে a, b, ও c হল ত্রিভুজের বাহুত্রয়ের দৈর্ঘ্য, ও α, β, ও γ হল বাহুত্রয়ের বিপরীত কোণ (উপরের চিত্র দেখুন) এবং R হল ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ।

সাধারণত এই সূত্র সূক্ষ্মকোণী ত্রিভুজের বাহুর দৈর্ঘ্য নির্ণয়ে ব্যবহার করা হয়।

উদাহরণ

পরিবৃত্তসহ ত্রিভুজ

চিত্রানুসারে S হল ত্রিভুজের ক্ষেত্রফল।

নিম্নে কিছু উদাহরণ দিয়ে বোঝানো হল:

উদাহরণ ১

চিত্র ১

প্রদত্ত: বাহু a = 20, বাহু c = 24, ও কোণ γ = 40°. কোণ α এর মান জানতে চাওয়া হয়েছে।

সাইন নিয়ম অনুসারে, $${\frac {\sin \alpha }{20}}={\frac {\sin(40^{\circ })}{24}}.$$ $$\alpha =\arcsin \left({\frac {20\sin(40^{\circ })}{24}}\right)\approx 32.39^{\circ }.$$

α এর আরেকটি মান α = 147.61° গৃহীত হয়নি কারণ এর জন্য α + β + γ > 180° হয়ে যাবে।

উদাহরণ ২

চিত্র ২

ত্রিভুজের দুটি বাহু a ও b এর দৈর্ঘ্য উভয়েরই x হয় ও তৃতীয় বাহুর দৈর্ঘ্য c হয়, a, b, ও c এর বিপরীত কোণ তিনটি α, β, ও γ হয় তবে $${\begin{aligned}&\alpha =\beta ={\frac {180^{\circ }-\gamma }{2}}=90^{\circ }-{\frac {\gamma }{2}}\\[6pt]&\sin \alpha =\sin \beta =\sin \left(90^{\circ }-{\frac {\gamma }{2}}\right)=\cos \left({\frac {\gamma }{2}}\right)\\[6pt]&{\frac {c}{\sin \gamma }}={\frac {a}{\sin \alpha }}={\frac {x}{\cos \left({\frac {\gamma }{2}}\right)}}\\[6pt]&{\frac {c\cos \left({\frac {\gamma }{2}}\right)}{\sin \gamma }}=x\end{aligned}}$$

পরিবৃত্তের সাথে সম্পর্ক

সূত্রানুসারে, বাহু ও তাদের বিপরীত কোণের সাইনের অনুপাত সর্বদা পরিব্যাসার্ধের দ্বিগুণের সমান।

প্রমাণ

ত্রিভুজ ADB বৃত্তের কেন্দ্রগামী। d হল বৃত্তটির ব্যাস

$\angle AOD=$ $180^{\circ }$ সুতরাং, $\angle ABD=90^{\circ }$ (অর্ধবৃত্তস্থ কোণ সর্বদা সমকোণ হয়)।

$$\sin {\delta }={\frac {c}{2R}},$$ যেখানে $R={\frac {d}{2}}$

${\gamma }={\delta }$ (যেহেতু সমবৃত্তাংশস্থ কোণ সর্বদা সমান হয়)। সুতরাং, $$\sin {\delta }=\sin {\gamma }={\frac {c}{2R}}$$

অনুরূপে প্রমাণ করা যায়,

${\frac {a}{\sin {\alpha }}}={\frac {b}{\sin {\beta }}}={\frac {c}{\sin {\gamma }}}=2R$

আরও দেখুন

• কোসাইনের সূত্র

বহিঃসংযোগ

• Hazewinkel, Michiel, সম্পাদক (২০০১), "Sine theorem", Encyclopedia of Mathematics, Springer Science+Business Media, আইএসবিএন 978-1-55608-010-4 উদ্ধৃতি টেমপ্লেট ইংরেজি প্যারামিটার ব্যবহার করেছে (link)
• The Law of Sines at cut-the-knot
• Degree of Curvature
• Finding the Sine of 1 Degree
• Generalized law of sines to higher dimensions