আলোর প্রতিসরণ
পদার্থবিজ্ঞানে প্রতিসরণ বলতে একটি তরঙ্গের পথ পরিবর্তনকে বোঝায়; যখন এটি একটি মাধ্যম থেকে অন্য মাধ্যমে যায়।[১] তরঙ্গের গতির পরিবর্তন বা মাধ্যমের পরিবর্তনের কারণে পথ পরিবর্তন হতে পারে।[২] আলোর প্রতিসরণ হতে সবচেয়ে বেশি দেখা যায়, তবে অন্যান্য তরঙ্গ যেমন শব্দ তরঙ্গ এবং জলতরঙ্গেও প্রতিসরণ হতে দেখা যায়। একটি তরঙ্গ কতটা প্রতিসৃত হয় তা তরঙ্গের গতির পরিবর্তন এবং গতির পরিবর্তনের দিকের সাপেক্ষে তরঙ্গের বিস্তারের প্রাথমিক দিক দ্বারা নির্ধারিত হয়।

আলোর প্রতিসরণের ঘটনা স্পষ্টভাবে দৃশ্যমান হয় যখন আলোকরশ্মি ০° ও ৯০° ব্যতীত অন্য যেকোনো কোণে মাধ্যমদ্বয়ের বিভেদতলে পড়ে। আলোর ক্ষেত্রে প্রতিসরণ স্নেলের সূত্র অনুসরণ করে, যা বিবৃত করে যে একটি জোড়া নির্দিষ্ট মাধ্যমের জন্য, আপতন θ1 ও প্রতিসরণ কোণের θ2 সাইনের অনুপাত মাধ্যমদ্বয়ের তরঙ্গ বেগের অনুপাতের (v1 / v2) সমান, সমতুল্যভাবে, মাধ্যমদ্বয়ের প্রতিসরাঙ্কের (n2 / n1) সমান।[৩]
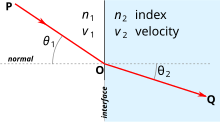
মূলত মাধ্যমগুলোর ঘনত্বের পার্থক্যের জন্যই আলোর প্রতিসরণ ঘটে থাকে। আলো যদি হালকা মাধ্যম (যেমন বায়ু) থেকে ঘন মাধ্যমে (যেমন পানি) প্রবেশ করে, তাহলে আলোকরশ্মি বিভেদ তল হতে অভিলম্বের দিকে বেঁকে যায়। আবার যদি আলো ঘন হতে হালকা মাধ্যমে আপতিত হয়, তাহলে আলো বিভেদ তল হতে অভিলম্ব থেকে দূরে সরে আসে।
আলোক প্রিজম ও লেন্স মানুষের চোখের মতো আলোর পথ পরিবর্তন করতে প্রতিসরণ ব্যবহার করে। পদার্থের প্রতিসরাঙ্ক আলোর তরঙ্গদৈর্ঘ্যের সাথে পরিবর্তিত হয়,[৪] এবং এইভাবে প্রতিসরণ কোণও একইভাবে পরিবর্তিত হয়। একে বিচ্ছুরণ বলা হয় এবং এর কারণে প্রিজম ও রংধনুতে সাদা আলোর উপাদান বর্ণালীয় রঙে ভাগ হয়ে যায়।[৫]
সাধারণ ব্যাখ্যা
সম্পাদনাপ্রতিসরণের সঠিক ব্যাখ্যায় দুটি পৃথক অংশ জড়িত, উভয়ই আলোর তরঙ্গ ধর্মের ফলাফল।
- ভ্যাকিউয়াম ব্যতীত অন্য কোনো মাধ্যমে (যেমন বায়ু, কাচ বা পানি) চলার সময় আলো ধীর হয়ে যায়। এটি বিক্ষিপ্ত বা শোষণের কারণে নয়, বরং একটি তড়িচ্চুম্বকীয় দোলক হিসাবে আলো নিজেই অন্যান্য বৈদ্যুতিক আধানযুক্ত কণা যেমন- ইলেকট্রনকে দোলন প্রদান করে। দোদুল্যমান ইলেকট্রনগুলো তাদের নিজস্ব তড়িচ্চুম্বকীয় তরঙ্গ নির্গত করে যা মূল আলোক তরঙ্গের সাথে মিথস্ক্রিয়া করে। এর ফলে সৃষ্ট "সম্মিলিত" তরঙ্গে তরঙ্গের প্যাকেট থাকে যা একজন পর্যবেক্ষককে ধীর গতিতে অতিক্রম করে। আলো কার্যকরভাবে ধীর হয়ে যায়। যখন আলো একটি ভ্যাকিউয়ামে ফিরে আসে এবং কাছাকাছি কোনো ইলেকট্রন না থাকে, তখন এই ধীরগতির প্রভাব শেষ হয়ে যায় এবং এর গতি c-এ (শূন্য মাধ্যমে আলোর বেগ) ফিরে আসে।
- যখন আলো একটি কোণে একটি ধীর মাধ্যমে প্রবেশ করে, তখন তরঙ্গমুখের এক দিক অন্যটির আগে ধীর হয়ে যায়। আলোর এই অপ্রতিসম ধীরগতির কারণে এটি তার চলার পথে কোণ পরিবর্তন করে। যথন আলো ধ্রুবক বৈশিষ্ট্যসহ নতুন মাধ্যমে পুনরায় প্রবেশ করে, তখন এটি আবার একটি সরল রেখায় চলতে থাক্র।
প্রতিসরাঙ্ক
সম্পাদনাপ্রতিসরাঙ্ক(Refractive Index):একজোড়া নির্দিষ্ট মাধ্যমে এবং কোন একটি নির্দিষ্ট বর্ণের আলোকরশ্মি এক মাধ্যম থেকে অপর মাধ্যমে প্রতিসৃত হলে যদি আপতন কোন এবং প্রতিসরণ কোন হয় তাহলে যে ধ্রুব সংখ্যা হয় তাকে বলা হয় ওই বর্ণের আলোর জন্য প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক।
প্রতিসরাঙ্ক হলো কোন আলোকীয় মাধ্যমের উপাদানের এমন একটি ধর্ম যার মানের উপর ওই মাধ্যমে প্রবেশ করা অর্থাৎ প্রতিসৃত আলোকরশ্মির গতির অভিমুখে এবং ওই মাধ্যমের আলোর বেগের মান নির্ভর করে। দুটি সমজাতীয় রাশির অনুপাত হওয়ায় প্রতিসরাঙ্ক একটি একক বিহীন সংখ্যা মাত্র প্রতিসরাঙ্ককে দু ভাবে বিভক্ত করা যেতে পারে। যথা:
১। আপেক্ষিক প্রতিসরাঙ্ক:
সম্পাদনাকোনো নির্দিষ্ট রংয়ের আলো যখন এক স্বচ্ছ মাধ্যম থেকে অন্য স্বচ্ছ মাধ্যমে তির্যকভাবে প্রবেশ করে তখন আপতন কোণ ও প্রতিসরণ কোণের সাইনের অনুপাত যে ধ্রুবক সংখ্যা হয় তাকে প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক (Relative Refractive index) বলে। উদাহরণস্বরূপ: যখন আলোকরশ্মি 'a' মাধ্যম থেকে 'b' মাধ্যমে প্রবেশ করে তখন আপতন কোণের সাইন ও প্রতিসরণ কোণের সাইনের অনুপাতকে বলা হবে 'a মাধ্যমের সাপেক্ষে 'b' মাধ্যমের প্রতিসরণাঙ্ক। এখন 'a' মাধ্যমে আপতন কোণ যদি p এবং 'b' মাধ্যমে প্রতিসরণ কোণ যদি q হয় তাহলে 'a' মাধ্যমের সাপেক্ষে 'b' মাধ্যমের প্রতিসরণাঙ্ক হবে:
- aηb =
২। পরম প্রতিসরাঙ্ক:
সম্পাদনাকোনো নির্দিষ্ট রংয়ের আলো যখন শূন্য মাধ্যম থেকে কোন স্বচ্ছ মাধ্যমে তির্যকভাবে প্রবেশ করে তখন আপতন কোণ ও প্রতিসরণ কোণের সাইনের অনুপাতকে উক্ত মাধ্যমটির পরম প্রতিসরাঙ্ক (Absolute Refractive Index) বলে। অর্থাৎ শূন্য মাধ্যমে কোন নির্দিষ্ট রংয়ের আলোকরশ্মির আপতন কোন p এবং অন্য মাধ্যমটিতে (ধরি, মাধ্যমটি y) প্রতিসরণ কোণ q হলে, উক্ত y মাধ্যমটির পরম প্রতিসরণাঙ্ক হবে:
- ηy =
আলোকরশ্মির বেগ ও প্রতিসরাঙ্কের সম্পর্ক
সম্পাদনাআমরা জানি, শূন্য মাধ্যমে আলোর বেগ সেকেন্ডে 2.99792458×108। আমাদের দৈনন্দিন জীবনে আমরা সেকেন্ডে 3 লক্ষ কিলোমিটার বেগ ধরে নিই। এতে তেমন কোনো সমস্যা হয় না। যাই হোক,আমরা এক্ষেত্রে ধরে নিই,আলোর বেগ সেকেন্ডে 3 লক্ষ কিলোমিটার। শূন্য মাধ্যমেই আলোর বেগ সবচেয়ে বেশি। আলোক রশ্মি শূন্য মাধ্যম থেকে কোনো মাধ্যমে প্রবেশ করলে আলোর বেগ কমে যায়। শূন্য মাধ্যম থেকে সেই মাধ্যমে আলোর বেগ যতগুণ কমে যায় সেটার পরিমাণই হচ্ছে শূন্য মাধ্যমের সাপেক্ষে সেই মাধ্যমের প্রতিসরনাঙ্ক।
ধরি, শূন্য মাধ্যম= a, অপর একটি মাধ্যম= b ।
তাহলে উপরের শর্তানুযায়ী,
aηb= (এখানে c হল শূন্য মাধ্যমে আলোর বেগ)
অর্থাৎ, ηb/ηa = ca / cb
আমাদের জানামতে, শূন্য মাধ্যমের (a মাধ্যমের) প্রতিসরাঙ্ক 1
∴ ηb= ca / cb
এই সূত্র ব্যবহার করে কোনো মাধ্যমের প্রতিসরাঙ্ক নির্ণয় করা যায়।
এই থেকেও এটিও বোঝা যায় যে, আলোর বেগ ও প্রতিসরাঙ্কের মধ্যে পরস্পর ব্যস্ত সম্পর্ক বিদ্যমান।
প্রতিসরণের সূত্র
সম্পাদনাআলোর প্রতিসরণের ওপর দুটি সূত্র বিশেষভাবে উল্লেখযোগ্য, যথা:
- আপতিত রশ্মি, প্রতিসরিত রশ্মি এবং আপতন বিন্দুতে বিভেদতলের উপর অঙ্কিত অভিলম্ব একই সমতলে অবস্থান করে।[৬]
- স্নেলের সূত্র: একজোড়া নির্দিষ্ট মাধ্যম এবং একটি নির্দিষ্ট বর্ণের আলোর জন্য, আপতন কোণের সাইন (sin) এবং প্রতিসরণ কোণের সাইনের (sin) অণুপাত সর্বদা ধ্রুবক থাকে। ১৬২০ সালে হল্যান্ডের বিজ্ঞানী স্নেল (Willebrord Snellius) সর্বপ্রথম এ সূত্র প্রকাশ করেন। তাই এ সূত্রটিকে স্নেলের সূত্রও বলা হয়।[৬]
অর্থাৎ, আপতন কোন , প্রতিসরণ কোন হলে, = ধ্রুবক। এই ধ্রুবক কে গ্রিক বর্ণমালার 'μ' দিয়ে চিহ্নিত করা হয়।
- প্রথম মাধ্যমের পরম প্রতিসরাঙ্ক n1, দ্বিতীয় মাধ্যমের পরম প্রতিসরাঙ্ক n2, আপতন কোণ θ1, প্রতিসরণ কোণ θ2 হলে, ফার্মাটেরনীতি অনুযায়ী । এক্ষেত্রে d²t/dx²>0 সুতরাং,সময় ন্যূনতম
সংকট কোণ ও আলোর পূর্ণ অভ্যন্তরীণ প্রতিফলন
সম্পাদনানির্দিষ্ট রঙের আলোক রশ্মি ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রতিসরিত হওয়ার সময় আপতন কোণের যে মানের জন্য প্রতিসরণ কোণের মান এক সমকোণ হয় অর্থাৎ প্রতিসরিত রশ্মি বিভেদ তল ঘেঁষে চলে যায় তাকে ঐ রঙের জন্য হালকা মাধ্যমের সাপেক্ষে ঘন মাধ্যমের সংকট কোণ বা ক্রান্তি কোণ (critical angle) বলে।
সংকট কোণ বা ক্রান্তি কোণকে θc দ্বারা প্রকাশ করা হয়। θc = sin-1 (η2/η1)
নিম্নে এর প্রমাণ দেওয়া হলো।
➤প্রমাণ:
আমরা জানি, পূর্ণ অভ্যন্তরীণ প্রতিফলন হওয়ার জন্য আলোকরশ্মিকে ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রবেশ করতে হয়।
ধরি, ঘন মাধ্যম = 1, হালকা মাধ্যম= 2 ।
আলোকরশ্মি 1 মাধ্যমে i কোণে আপতিত হয়েছে। এর ফলে প্রতিসরিত রশ্মিটি বিভেদতল ঘেষে প্রতিসরিত হয়েছে।
যেহেতু বিভেদতলে আলোকরশ্মি প্রতিসরিত হয়েছে, তাই প্রতিসরণ কোণের মান, r=90° এবং i কোণে আলো আপতিত হওয়ার কারণে এটি বিভেদতল ঘেষে প্রতিফলিত হয়েছে। সুতরাং i= θc
প্রতিসরণের সূত্র থেকে আমরা পাই,
প্রথম মাধ্যমের প্রতিসরাঙ্ক × কোণের সাইন = দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক × কোণের সাইন
বা, η1 sin i = η2 sin r
বা, η1 sinθc = η2 sin90°
বা, η1 sinθc = η2 [∵ sin90°=1]
বা, sinθc = η2 / η1
বা, θc = sin−1 ( η2 / η1 )
সূত্র ব্যবহার করে সংকট কোণের মান নির্ণয় করা যায়।(প্রমাণিত)
পূর্ণ অভ্যন্তরীণ প্রতিফলন হলো সেই ঘটনা ঘটে যখন আলো কেবলমাত্র ঘন মাধ্যম থেকে হালকা মাধ্যমে প্রবেশের সময়ে দুই মাধ্যমের বিভেদতলে অভিলম্বের সাথে সংকট কোণের চেয়ে বেশি কোণে আপতিত হয়ে সম্পূর্ণ আলো পূর্বের মাধ্যমে প্রতিফলিত হয়। যেহেতু আলোর আপতন কোণ সংকট কোণের সমান হলে প্রতিফলিত রশ্মি দুই মাধ্যমের বিভেদতল ঘেঁষে যায়, সেহেতু আলো সংকট কোণের চেয়ে বেশি কোণে আপতিত হলে তা পরবর্তী মাধ্যমে প্রবেশ না করে পূনরায় পূর্বের মাধ্যমে ফিরে আসবে।
দৈনন্দিন জীবনে প্রতিসরণ
সম্পাদনাআমাদের দৈনন্দিন জীবনের অনেক স্থানে আলোর প্রতিসরণ দেখা যায়। এটি পানির পৃষ্ঠের নিচে বস্তুগুলোকে তার প্রকৃত অবস্থানের চেয়ে কাছাকাছি দেখায়। এর উপর ভিত্তি করেই আলোক লেন্স তৈরি করা হয়, যেটি চশমা, ক্যামেরা, বাইনোকুলার, অণুবীক্ষণ যন্ত্র এবং মানুষের চোখের মতো যন্ত্রাংশে ব্যবহৃত হয়। রংধনু এবং মরীচিকাসহ কিছু প্রাকৃতিক আলোক ঘটনার জন্যও প্রতিসরণ দায়ী।
- জেলের মাছ ধরার ক্ষেত্রেও প্রতিসরণের জন্য অনেক সময় জেলে মাছ ধরতে ব্যর্থ হন। মাছ থেকে আলোকরশ্মি জল (ঘন মাধ্যম) থেকে বায়ুতে (লঘু মাধ্যম) আসার সময় প্রতিসরণ ঘটে ও আলোকরশ্মি অভিলম্ব থেকে দূরে সরে যায়। সেই রশ্মি জেলের চোখে পৌঁছালে তিনি মাছকে আপাত দৃষ্টিতে কিছুটা উপরে দেখেন। তাই মাছ যেখানে দেখতে পান তার কিছুটা নীচে বর্শি দিয়ে আঘাত করেন।
- মরুভূমিতে মরীচিকা সৃষ্টি হয় প্রতিসরণের জন্যই। এছাড়া গ্রীষ্মে রাস্তা দূর থেকে দেখলে ভেজা মনে হয় একই কারণবশত।
- সকালে সূর্য উঠার সময় পূর্ব আকাশে এবং দুপুরে সূর্য অস্ত যাওয়ার সময় পশ্চিম আকাশে লাল আভা দেখা যায়, তাতে প্রতিসরণ সাহায্য করে।
- আকাশে তারার ঝিকমিক প্রতিসরণের ফলে সৃষ্টি হয়। আসলে বহু দূরের নক্ষত্রগুলির আলো যখন পৃথিবীর বায়ুমণ্ডল ভেদ করে আমাদের চোখে আসে, তখন বায়ুমণ্ডলের বিভিন্ন স্তর এর বিভিন্ন রকম উষ্ণতা হওয়ার জন্য প্রতিসরাঙ্কও বিভিন্ন হয়। এর জন্য সেই আলোর প্রতিসরণ ঘটে এবং বারবার প্রতিসরাঙ্ক পরিবর্তন হওয়ার ফলে বারবার প্রতিসরণ ঘটতে থাকে এবং আমাদের চোখে এসে পড়ে ও আমাদের মনে হয় তারাটি ঝিকমিক করছে।
- আলোর বিচ্ছুরণ প্রতিসরণের ফলে সৃষ্ট। প্রিজমের মধ্যে বিভিন্ন আলোর প্রতিসরাঙ্ক ও বেগ বিভিন্ন হওয়ার জন্য বিচ্ছুরিত হয়ে যায়।
- মানুষের চোখের লেন্স (প্রাকৃতিক লেন্স) আলোর প্রতিসরণ ঘটিয়ে রেটিনায় প্রতিবিম্ব উৎপন্ন করে। বিভিন্ন চশমায় ব্যবহৃত লেন্স প্রতিসরণ ঘটিয়ে দেখতে সাহায্য করে।
যান্ত্রিক তরঙ্গ
সম্পাদনাজলতরঙ্গ
সম্পাদনাপানির তরঙ্গ অগভীর পানিতে ধীর গতিতে চলাচল করে। একে ব্যবহার করে লহরী ট্যাঙ্কে প্রতিসরণ প্রদর্শন করতে করা যেতে পারে এবং ব্যাখ্যা করা যায় যে কেন একটি উপকূলে তরঙ্গ একটি অভিলম্বের কাছাকাছি তীরে আঘাত করে। তরঙ্গগুলি গভীর পানি থেকে তীরের কাছাকাছি অগভীর পানিতে চলাচল করার সময়, এগুলো এদের চলনের মূল দিক থেকে উপকূলরেখার আরও সাধারণ কোণে প্রতিসৃত হয়।[৭]
শব্দতরঙ্গ
সম্পাদনাজলতলের শব্দবিজ্ঞানে প্রতিসরণ বলতে একটি শব্দ রশ্মির বেঁকে যাওয়াকে বোঝায়, যার ফলে রশ্মি বেগের একটি নথিমাত্রার মধ্য দিয়ে শব্দের একটি নির্দিষ্ট বেগের এলাকা থেকে ভিন্ন বেগের একটি এলাকায় চলে যায়। রশ্মি বেঁকে যাওয়ার পরিমাণ নির্ভর করে শব্দের বেগের পার্থক্যের উপর, অর্থাৎ তাপমাত্রা, লবণাক্ততা এবং পানির চাপের তারতম্যের উপর।[৮] পৃথিবীর বায়ুমণ্ডলেও অনুরূপ ঘটনার প্রভাব পাওয়া যায়। বায়ুমণ্ডলে শব্দের প্রতিসরণের ঘটনা বহুশতাব্দী যাবত জ্ঞাত;[৯] যাইহোক, ১৯৭০-এর দশকের গোড়ার দিকে, নিম্ন বায়ুমণ্ডলে শব্দ রশ্মির বেঁকে যাওয়ার আবহাওয়াগত প্রভাব মোকাবেলায় শহরাঞ্চলের মহাসড়ক ও শব্দ রোধকের নকশার মাধ্যমে এই প্রভাবের ব্যাপক বিশ্লেষণ প্রচলিত হয়।[১০]
আরও দেখুন
সম্পাদনাতথ্যসূত্র
সম্পাদনা- ↑ ড. গিয়াস উদ্দিন আহমেদ; ড. মমিনুল হক; রাশিদুল হাসান; মাহেরা আহমেদ (জুন, ২০০৫)। "আলোর প্রতিসরণ"। উচ্চ মাধ্যমিক পদার্থবিজ্ঞান বই (দ্বিতীয় পত্র) (ষষ্ঠ সংস্করণ)। ঢাকা: মেট্রো পাবলিকেন্স। পৃষ্ঠা ২৯৯–৩৬৪। এখানে তারিখের মান পরীক্ষা করুন:
|তারিখ=(সাহায্য); - ↑ The Editors of Encyclopaedia Britannica। "Refraction"। Encyclopaedia Britannica। সংগ্রহের তারিখ ২০১৮-১০-১৬।
- ↑ Born and Wolf (১৯৫৯)। Principles of Optics। New York, NY: Pergamon Press INC.। পৃষ্ঠা 37।
- ↑ R. Paschotta, article on chromatic dispersion ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০১৫-০৬-২৯ তারিখে in the Encyclopedia of Laser Physics and Technology ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০১৫-০৮-১৩ তারিখে, accessed on 2014-09-08
- ↑ Carl R. Nave, page on Dispersion ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০১৪-০৯-২৪ তারিখে in HyperPhysics ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০০৭-১০-২৮ তারিখে, Department of Physics and Astronomy, Georgia State University, accessed on 2014-09-08
- ↑ ক খ M. Nelkon (১৯৯৩)। "Light"। Principles of Physics (10th সংস্করণ)। Singapore: SHING LEE PUBLISHERS PTE LTD.। পৃষ্ঠা 272–273। আইএসবিএন 9971616688।
- ↑ "Shoaling, Refraction, and Diffraction of Waves"। University of Delaware Center for Applied Coastal Research। ২০০৯-০৪-১৪ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২০০৯-০৭-২৩।
- ↑ Navy Supplement to the DOD Dictionary of Military and Associated Terms (পিডিএফ)। Department Of The Navy। আগস্ট ২০০৬। NTRP 1-02।
- ↑ Mary Somerville (1840), On the Connexion of the Physical Sciences, J. Murray Publishers, (originally by Harvard University)
- ↑ Hogan, C. Michael (১৯৭৩)। "Analysis of highway noise"। Water, Air, & Soil Pollution। 2 (3): 387–392। এসটুসিআইডি 109914430। ডিওআই:10.1007/BF00159677। বিবকোড:1973WASP....2..387H।
