দ্বিমিক সংখ্যাপদ্ধতি
বাইনারি সংখ্যা পদ্ধতি বা দ্বিমিক সংখ্যা পদ্ধতি (ইংরেজি: Binary number system) একটি সংখ্যা পদ্ধতি যাতে সকল সংখ্যাকে কেবলমাত্র ০ এবং ১ দিয়ে প্রকাশ করা হয়। এই সংখ্যা পদ্ধতির ভিত্তি দুই[১]। ডিজিটাল ইলেকট্রনিক যন্ত্রপাতির লজিক গেটে এই সংখ্যাপদ্ধতির ব্যাপক প্রয়োগ রয়েছে। তাছাড়া প্রায় সকল আধুনিক কম্পিউটারে বাইনারি সংখ্যা পদ্ধতি ব্যবহার করা হয়। বাইনারি পদ্ধতিতে প্রতিটি অঙ্ককে বিট বলা হয়।
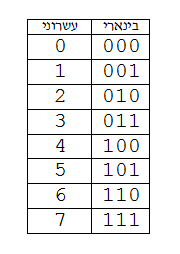
সংখ্যা পদ্ধতিকে সাধারণত ৪ ভাগে ভাগ করা হয়। (১) ডেসিমেল নাম্বার সিস্টেম, (২) বাইনারী নাম্বার সিস্টেম, (৩) অক্টাল নাম্বার সিস্টেম ও (৪) হেক্সা ডেসিমেল নাম্বার সিস্টেম। ডেসিমেল নাম্বার
সিস্টেমে অঙ্ক ১০ টি অর্থাৎ এর বেজ ১০ (১,২,৩,৪,৫,৬,৭,৮,৯,০)। অনুরূপভাবে বাইনারী নাম্বার সিস্টেমের বেজ ২ (১,০), অক্টাল নাম্বার সিস্টেমের বেজ ৮ (১,২,৩,৪,৫,৬,৭,০), হেক্সা ডেসিমেল নাম্বার সিস্টেমের বেজ ১৬(১,২,৩,৪,৫,৬,৭,৮,৯,A,B,C,D,E,F, ০ )।
ইতিহাস
সম্পাদনাবাইনারি সংখ্যাপদ্ধতির রূপান্তর
সম্পাদনা৫ এর বাইনারি (?)২
(৫)১০ কে বাইনারি বেজ অর্থাৎ ২ দ্বারা ভাগ করে অগ্রসর হতে হবে।[২]
৫÷২
ভাগফল ২ ভাগশেষ ১ (LSB কম গুরুত্বপূর্ণ বিট)
২÷২
ভাগফল ১ ভাগশেষ ০
১÷২
ভাগফল ০ ভাগশেষ ১ (MSB সর্বাধিক গুরুত্বপূর্ণ বিট)
ভাগশেষ গুলোকে MSB থেকে LSB হিসাবে সাজিয়ে নিতে হবে।
অর্থাৎ ১০১
(৫)১০=(১০১)২
আবার ১০১ এর ডেসিমেল মান অর্থাৎ দশমিক সংখ্যা হবে
১×২২+০×২১+১×২০
=১×৪+০×২+১×১
=৪+০+১
=৫
বাইনারি সংখ্যার যোগ : (নিয়ম)
0+0=0 ;
1+1=0,হাতে 1;
1 + 0 = 1;
0 + 1 = 1.
যেমন:
1010
(+)11
=1101 ( Ans).
তথ্যসূত্র
সম্পাদনা- ↑ ওয়েব সাইট, ১০ মিনিট স্কুল। "সংখ্যা পদ্ধতির ভিত্তি"। সংখ্যা পদ্ধতির ভিত্তি।
- ↑ পত্রিকা, নাগরিক ভয়েস। "নাগরিক ভয়েস পত্রিকা"। নাগরিক ভয়েস।
বহিঃসংযোগ
সম্পাদনা- A brief overview of Leibniz and the connection to binary numbers
- Binary System at cut-the-knot
- Conversion of Fractions at cut-the-knot
- Binary Digits at Math Is Fun
- Binary converter with direct access to bits ওয়েব্যাক মেশিনে আর্কাইভকৃত ২১ ফেব্রুয়ারি ২০১১ তারিখে
- How to Convert from Decimal to Binary at wikiHow
- Learning exercise for children at CircuitDesign.info
- Binary Counter with Kids
- “Magic” Card Trick
- Quick reference on Howto read binary
- Online converter for all types of binary numbers (including single and double precision IEEE754 numbers)
- Online numeral system converter[স্থায়ীভাবে অকার্যকর সংযোগ]
- বাইনারি সংখ্যা টিউটোরিয়াল