হিপ সর্ট
কম্পিউটার বিজ্ঞানে হিপসর্টটি একটি তুলনা ভিত্তিক বাছাইকরণ অ্যালগরিদম । হিপসর্টটি সিলেকশন সর্ট এর উন্নত ধরন হিসাবে বিবেচনা করা যেতে পারে:সিলেকশন সর্ট এর মতো হিপসর্টটি তার ইনপুটটিকে একটি সাজানো এবং একটি অসাজানো অঞ্চলে বিভক্ত করে এবং এটি পুনরাবৃত্তিকভাবে অসাজানো অঞ্চল থেকে বৃহত্তম উপাদানটি বের করে অঞ্চলটিকে ছোট করে এবং সাজানো অঞ্চলে সন্নিবেশ করে। সিলেকশন সর্ট এর মতো , হিপসর্টটি অসাজানো অঞ্চলের লিনিয়ার-সময় স্ক্যানের সাথে সময় নষ্ট করে না,বরং, প্রতিটি ধাপে সবচেয়ে বড় উপাদানটি আরও দ্রুত খুঁজে পেতে হিপসর্টটি সিলেকশন সর্ট এর উন্নত ধরনহিপসর্টটি অসাজানো অঞ্চলকে হিপ নামক ডেটা স্ট্রাকচারে বজায় রাখে। [১]
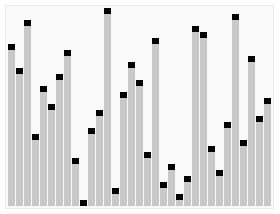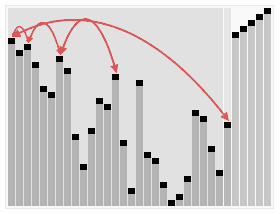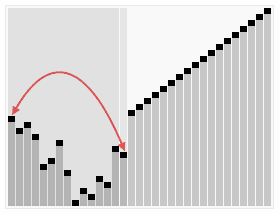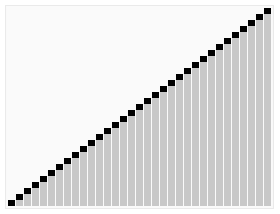 এলোমেলোভাবে অনুমতিপ্রাপ্ত মানের একটি অ্যারে বাছাই করে হিপসোর্টের একটি রান দেখানো হয়েছ. অ্যালগরিদমের প্রথম পর্যায়ে ,অ্যারে উপাদানগুলিকে হিপ বৈশিষ্ট্য পূরণ করার জন্য পুনরায় সাজানো হয়. প্রকৃত সর্টিং এর আগে, হিপ ট্রি কাঠামো চিত্রের জন্য সংক্ষেপে দেখানো হলো. | |
| শ্রেণী | Sorting algorithm |
|---|---|
| উপাত্ত সংগঠন | Array |
| প্রতিকূল অবস্থায় সময় | |
| অনুকূল অবস্থায় সময় | (distinct keys) or (equal keys) |
| সাধারণ অবস্থায় সময় | |
| প্রতিকূল অবস্থায় গৃহীত মেমরি | total auxiliary |
যদিও বেশিরভাগ মেশিনে একটি সু-বাস্তবায়িত কুইক সর্ট এর তুলনায় অনুশীলনে হিপসর্টটি কিছুটা ধীর গতিযুক্ত, এটির ব্যবহারে সবচেয়ে বাজে রানটাইমের ক্ষেত্রে O(এন লগ এন ) সুবিধা রয়েছে। হিপসর্ট একটি ইন-প্লেস অ্যালগরিদম, তবে এটি কোন স্থিতিশীল সর্ট ও নয়।
হিপসর্টটি ১৯৪64 সালে জে.ডাব্লিউ .জে উইলিয়ামস আবিষ্কার করেছিলেন। [২] এই সময়ে হিপের ও সূচনা হয় এবং উইলিয়ামস নিজস্ব একটি দরকারী ডেটা স্ট্রাকচার হিসাবে হিপকে উপস্থাপণ করেন । [৩] একই বছরে, আর.ডাব্লিউ .ফ্লোয়েড ট্রি হিপসর্টটি সিলেকশন সর্ট এর উন্নত ধরন হিসাবে বিবেচনা করা যেতে পারে: সিলেকশন সর্ট এর মতো হিপসর্টটি তার ইনপুটটিকে একটি সাজানো এবং একটি অসাজানো অঞ্চলে বিভক্ত করে এবং এটি পুনরাবৃত্তিকভাবে অসাজানো অঞ্চল থেকে বৃহত্তম উপাদানটি বের করে অঞ্চলটিকে ছোট করে এবং সাজানো অঞ্চলে সন্নিবেশ করে।সর্ট অ্যালগরিদমে নিজের গবেষণা অব্যহত রেখে একটি উন্নত সংস্করণ প্রকাশ করেছেন যা একটি অ্যারেকে ইন-প্লেস সর্ট করতে পারে।
ওভারভিউ
সম্পাদনাহিপসর্ট অ্যালগরিদমকে দুটি ভাগে ভাগ করা যায়।
প্রথম ধাপে, একটি হিপ ডেটা থেকে তৈরি করা হয় ( দেখুন বাইনারি হিপ এবং হিপ তৈরি)। হিপকে প্রায়ই সম্পূর্ণ বাইনারি ট্রি এর বিন্যাস সহ একটি অ্যারেতে রাখা হয়। সম্পূর্ণ বাইনারি ট্রি বাইনারি ট্রি কাঠামোটিকে অ্যারে ইনডেক্স গুলিতে ম্যাপ করে। প্রতিটি অ্যারে ইনডেক্স একটি নোড প্রতিনিধিত্ব করে।নোডের পিতামাতা, বাম চাইল্ড শাখা বা ডান চাইল্ড শাখার ইনডেক্স এগুলো সাধারণ অভিব্যক্তি। শূন্য-ভিত্তিক অ্যারের জন্য রুট নোডকে 0 ইনডেক্সে সর্ট করা হয়; যদি i বর্তমান নোডের ইনডেক্স হয়, তবে
iParent(i) = floor((i-1) / 2) এখানে ফ্লোরু ফাংশন একটি বাস্তব সংখ্যাকে সবচেয়ে ক্ষুদ্রতম লিডিং ইন্টিজারে ম্যাপ করে. iLeftChild(i) = 2*i + 1 iRightChild(i) = 2*i + 2
দ্বিতীয় ধাপে, বার বার হিপ থেকে সবচেয়ে বড় উপাদানটিকে (হিপ এর রুট) সরিয়ে এবং অ্যারেতে প্রবেশ করিয়ে একটি সর্টেড অ্যারে তৈরি করা হয়। হিপ বৈশিষ্ট্য বজায় রাখতে প্রতিটি অপসারণের পরে হিপ পরিবর্তন করা হয়। একবার সমস্ত অবজেক্ট হিপ থেকে সরানো হয়ে গেলে যে অ্যারেটি পাবো সেটি সর্টেড অ্যারে হবে।
হিপসর্ট দিয়ে একটি অ্যারে ব্যবহার করেই সর্ট এর কাজ করা যায় । অ্যারেটিকে দুটি ভাগে ভাগ করা যায়, সর্টেড অ্যারে এবং হিপ। অ্যারে হিসাবে হিপ এর স্টোরেজটি এখানে চিত্রে দেখানো হলো। হিপ এর ইনভ্যারিয়্যান্ট প্রতিটি নিষ্কাশনের পরে সংরক্ষণ করা হয়, তাই নিষ্কাশন পদ্ধতিটাই একমাত্র বিবেচনার বিষয়।
অ্যালগরিদম
সম্পাদনাহিপসর্ট অ্যালগরিদমে প্রথমে লিস্টকে মাক্স হিপে পরিণত করা হয় । অ্যালগরিদমটি তারপরে বারবার লিস্টের প্রথম মানটিকে সর্বশেষ মান দিয়ে প্রতিস্থাপন করে, এভাবে হিপ অপারেশনে বিবেচিত মানের পরিসরকে এক এক করে হ্রাস করে এবং নতুন প্রথম মানটিকে হিপের নিজস্ব অবস্থানে স্থানপরিবর্তন করে। বিবেচিত মানগুলির ব্যাপ্তি দৈর্ঘ্যের মান এক না হওয়া পর্যন্ত অপারেশনটি পুনরাবৃত্তিকভাবে চলতে থাকে।
পদক্ষেপগুলি হ'ল:
- লিস্টের বিল্ডম্যাক্সহিপ () ফাংশনটি কল করুন। এটি হেপিফাই () হিসাবেও পরিচিত, এটি অর্ডার (এন) অপারেশনে লিস্ট থেকে একটি হিপ তৈরি করে।
- লিস্টের প্রথম মানকে শেষ মান দিয়ে প্রতিস্থাপন করুন । লিস্টের বিবেচিত পরিসরকে এক এক করে হ্রাস করুন।
- নতুন প্রথম মানটিকে এর যথাযথ ইনডেক্সে হিপের মধ্যে বসাতে লিস্টে শিফ্টডাউন () ফাংশনটি কল করুন।
- লিস্টের বিবেচিত পরিসরে একটি উপাদান না থাকা পর্যন্ত পদক্ষেপ(2) এ ফিরে যান।
বিল্ডম্যাক্সহিপ () অপারেশনটি একবার চালানো হয় এবং এটি অর্ডার (এন) এ সম্পন্ন হয়। শিফ্টডাউন () ফাংশনটি ও O(log এন ) এ সম্পন্ন হয় এবং এন বার কল করা হয় ।সুতরাং, এই অ্যালগরিদমের কার্যকারিতা হ'ল O(এন + এন লগ এন ) = O ( এন লগ এন ) ।
স্যুডোকোড
সম্পাদনাস্যুডোকোডে অ্যালগরিদমটি প্রয়োগ করার জন্য নিম্নলিখিতটি একটি সহজ উপায় আছে। অ্যারেগুলি শূন্য-ভিত্তিক এবং অ্যারের দুটি উপাদান বিনিময় করতে swap ব্যবহার করা হয়। আন্দোলন 'ডাউন' অর্থ রুট থেকে লিভ্সের দিকে যাওয়া, বা নিম্ন ইনডেক্স থেকে উচ্চতর ইনডেক্সের দিকে যাওয়া। মনে রাখবেন যে সর্টের সময়, বৃহত্তম উপাদানটি a[0] তে হিপের রুট এ থাকে,সর্ট শেষে, বৃহত্তম উপাদানটি a[end] হয় ।
heapsort(a, count) ফাংশনটির পদ্ধতি হলো;
ইনপুট: একটি count দৈর্ঘ্যের আনসর্টেড অ্যারে
(হিপ অ্যারেটি তৈরি করুন যাতে বৃহত্তম উপাদানটি রুটে থাকে)
heapify(a, count)
(নিচের লুপটি ইনভ্যারিয়্যান্ট বজায় রাখে যেন a[0:end] হিপ হয় এবং end এর আগ পর্যন্ত প্রত্যেকটি উপাদান এর সামনের উপাদান থেকে বৃহত্তর হয়(তাই a[end:count] সর্টেড থাকে))
end ← count - 1
while end > 0 do
(a[0] হচ্ছে রুট এবং বৃহত্তম উপাদান। swap একে সর্টেড উপাদানগুলোর সামনে নিয়ে যায় )
swap(a[end], a[0])
(হিপের দৈর্ঘ্য এক কমানো হয়েছ)
end ← end - 1
(swap হিপ বৈশিষ্ট্যকে নষ্ট করে ফেলে, তাই একে পুনরুদ্ধার করুন)
siftDown(a, 0, end)
<i>সর্টিং</i> হিপিফাই এবং শিফ্টডাউন এই দুইটি প্রক্রিয়া মাধ্যমে সম্পন্ন করে । হিপিফাই বাস্তবায়নের জন্য সাধারণ স্থানে থাকা হিপ তৈরিতে while লুপ
('a' এর উপাদানগুলিকে হিপ অর্ডারে ইন-প্লেসে রাখুন)
প্রক্রিয়া heapify (a, count) হলঃ
(শুরুটি শেষ প্যারেন্ট নোডের 'a' ইনডেক্সে বসানো হয়)
(0-ভিত্তিক অ্যারেতে সর্বশেষ উপাদানটি count -1 ইনডেক্সে রয়েছে; সেই উপাদানটির প্যারেন্ট সন্ধান করুন)
start ← iParent(count-1)
while start ≥ 0 do
(start ইনডেক্স নোডটি যথাযথ জায়গায় শিফ্টডাউন ফাংশন ব্যবহার করেসরিয়ে নিন যাতে start ইনডেক্সের নীচে সকল নোড
হিপ অর্ডারে থাকে)
siftDown(a, start, count - 1)
(পরবর্তী প্যারেন্ট নোডে যান)
start ← start - 1
(রুটটি নীচে নেওয়ার পরে সমস্ত নোড / উপাদানগুলি হিপ অর্ডারে থাকে)
(হিপটি ঠিক করুন যার রুট উপাদান start ইনডেক্স রয়েছে , হিপটি যে নোডে রুটেড আছে চাইল্ডগুলি বৈধ বলে ধরে নিবেন)
প্রক্রিয়া siftDown(a, start, end)) হলঃ
root ← start
while iLeftChild(root) ≤ end do (যতক্ষণ না কমপক্ষে রুটের একটি চাইল্ড রয়েছে)
child ← iLeftChild(root) (রুটের বাম চাইল্ড)
swap ← root (রুটটি অদলবদল করতে চাইল্ডের উপর নজর রাখে)
if a[swap] < a[child] then
swap ← child
(যদি ডান চাইল্ড থাকে এবং সেই চাইল্ডটি আরও বড় হয়)
if child+1 ≤ end and a[swap] < a[child+1] then
swap ← child + 1
if swap = root then
(রুটটি সবচেয়ে বড় উপাদানকে ধারণ করে। যেহেতু আমরা ধরে নিই যে হিপটি যে নোডে রুটেড আছে চাইল্ডগুলি বৈধ, এর অর্থ আমরা কাজ শেষ)
return
else
swap(a[root], a[swap])
root ← swap (এখন চাইল্ডকে নীচে নামানো চালিয়ে যেতে শিফ্টডাউন প্রক্রিয়াটি পুনরাবৃত্তি করুন)
হিপিফাই পদ্ধতিটি <i id="mwbw">হিপ</i> বৈশিষ্ট্যটি প্রতিষ্ঠার জন্য ধারাবাহিকভাবে নীচের দিকে অগ্রসর হয়ে নীচ থেকে উপরে একটি হিপ নির্মাণ হিসাবে ভাবা যেতে পারে। একটি বিকল্প সংস্করণ আছে যা আরও বোধগম্য হতে পারে (নীচে দেখানো হয়েছে) সেটি হল হিপ টপ-ডাউন তৈরি করা এবং উপরের দিকে শিফ্ট করা । এই শিফ্টআপ সংস্করণটি খালি হিপ দিয়ে শুরু করে এবং ধারাবাহিকভাবে উপাদানগুলিকে সন্নিবেশ করে যেখানে উপরে বর্ণিতশিফ্টডাউন সংস্করণটি সম্পূর্ণ ইনপুট অ্যারেটিকে পরিপূর্ণ হিসেবে বিবেচনা করে তবে শেষ তুচ্ছ উপহিপ( শেষ প্যারেন্ট নোড) থেকে শুরু করে হিপকে ভাঙতে এবং মেরামত করতে থাকে ।
শিফ্টডাউন" সংস্করণ এবং "শিফ্টআপ" সংস্করণের মধ্যে সময়ের জটিলতার পার্থক্য।এছাড়াও, শিফ্টডাউন সংস্করণে O ( এন ) টাইম কমপ্লেক্সিটি রয়েছে, যখন নীচে উল্লেখিতশিফ্টডাউন সংস্করণে প্রতিটি উপাদান একবারে একটি করে সন্নিবেশ করার কারণে টাইম কমপ্লেক্সিটি হয় O ( এন লগ এন ) । [৪] এটি পাল্টা স্বজ্ঞাত হিসাবে মনে হতে পারে, এক নজরে, এটা স্পষ্ট যে আগেরটি তার লগারিথমিক-সময় শিফিং ফাংশনটিকে পরবর্তীর তুলনায় অর্ধেক কল করে; অর্থাৎ, এগুলি কেবল একটি ধ্রুবক ফ্যাক্টর দ্বারা পৃথক বলে মনে হয়, যা কখনই অ্যাসিম্পটোটিক বিশ্লেষণকে প্রভাবিত করে না।
কমপ্লেক্সিটির এই পার্থক্যের পিছনের অন্তর্দৃষ্টি উপলব্ধি করার জন্য, মনে রাখবেন যে কোনও একটি শিফ্টআপ কল চলাকালীন ঘটে যাওয়া swap সংখ্যা নোডের ডেপ্থ বৃদ্ধির সাথে সাথে বৃদ্ধি পায় যেখানে কল করা হয়। সমস্যা হ'ল একটি হিপে "shallow" নোডের তুলনায় "deep" নোডের সংখ্যা অনেক বেশি(তাত্পর্যপূর্ণভাবে) , যাতে হিপের নীচে বা এর কাছাকাছি নোডগুলিতে আনুমানিক লিনিয়ার সংখ্যক কল করার সময় শিফ্টআপ এর সম্পূর্ণ লগারিথমিক রানিং সময় থাকতে পারে । অন্যদিকে, যে কোনও শিফ্টআপ কল চলাকালীন ঘটে যাওয়া swap সংখ্যা যে নোডের উপরে কল করা হয় তার ডেপ্থ বৃদ্ধি সাথে সাথে হ্রাস পায় । সুতরাং, যখন শিফ্টডাউন হিপিফাই শুরু হয় এবং নীচের সবচেয়ে বেশি সংখ্যক নোড-স্তরসমূহ থেকেশিফ্টডাউনকে কল করে, প্রত্যেকবার শিফ্টিং কল করার সময় , সর্বাধিক swap এর সংখ্যা যে নোড থেকে শিফ্টিং কল করা হয় সে নোড থেকে "উচ্চতা" (হিপের নীচ থেকে) এর সমান হয় । অন্য কথায়, শিফ্টডাউনের প্রায় অর্ধেক কলগুলির মধ্যে সর্বাধিক মাত্র একটি swap হবে, তারপরে প্রায় চতুর্থাংশ কলগুলির মধ্যে কমপক্ষে দুইটি swap হবে ইত্যাদি .
হিপসর্ট অ্যালগরিদম নিজেই হিপিফাইয়ের উভয় সংস্করণ ব্যবহার করে টাইম কমপ্লেক্সিটি O ( এন লগ এন) রাখে।
প্রক্রিয়া heapify(a,count) হলঃ
(end রুটের প্রথম (বাম) চাইল্ডের ইনডেক্সে রাখা হয়)
end := 1
while end < count
( end ইনডেক্সের নোডকে যথাযথ স্থানে শিফ্টআপ করুনযাতে end ইনডেক্সের উপরের সমস্ত নোড হিপ অর্ডারে থাকে )
siftUp(a, 0, end)
end := end + 1 (সর্বশেষ নোডটিশিফ্টআপ করার পরেসমস্ত নোডগুলি হিপ অর্ডারে রয়েছে) প্রক্রিয়া siftUp(a, start, end) হলঃ ইনপুট: স্টার্ট সীমা নির্ধারণ করে কতটুকু হিপকেশিফ্ট করতে হবে। end হল যে নোডকেশিফ্টআপ করতে হবে। child := end while child > start parent := iParent(child)
if a[parent] < a[child] then(ম্যাক্সহিপ অর্ডারের বাইরে)
swap(a[parent], a[child])
child := parent (এখন চাইল্ডকে উপরের দিকে নিতেশিফ্টআপপ্রক্রিয়াটি পুনরাবৃত্তি করুন) else return
তথ্যসূত্র
সম্পাদনা- ↑ Skiena, Steven (২০০৮)। "Searching and Sorting"। The Algorithm Design Manual। Springer। পৃষ্ঠা 109। আইএসবিএন 978-1-84800-069-8। ডিওআই:10.1007/978-1-84800-070-4_4।
- ↑ Williams 1964
- ↑ Brass, Peter (২০০৮)। Advanced Data Structures। Cambridge University Press। পৃষ্ঠা 209। আইএসবিএন 978-0-521-88037-4।
- ↑ "Priority Queues"। ৯ সেপ্টেম্বর ২০২০ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ১০ সেপ্টে ২০২০।


