ভাগ
গণিতে ভাগ বা বিভাজন (বা পুনঃপুনঃ বিয়োগ) একটি বীজগাণিতিক ক্রিয়াপদ্ধতি (অপারেশন) যা '÷' অথবা '/' দ্বারা প্রকাশ করা হয়।
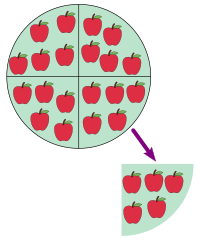
ভাগের গাণিতিক প্রকাশ
সম্পাদনানির্দিষ্টভাবে বলা যায় যদি দ্বার -কে গুণ করে পাওয়া যায়, অর্থাৎ হয় এবং যদি এই সমীকরণে হয়, তবে কে দ্বারা, ভাগ করলে পাওয়া যাবে। এটিকে নিচের মত করে লেখা যায়:
- ÷
উদাহরণস্বরূপ,
- যেহেতু,
উপরের সমীকরণে কে ভাজ্য, কে ভাজক এবং কে ভাগফল বলা হয়। অথবা ভাগের এই রাশিতে কে লব এবং কে হর বলা হয়।[১]
সাধারণত সবাই প্রাথমিক বিদ্যালয়েই যোগ, বিয়োগ, গুণের মত ভাগের ধারণাও অর্জন করে। দুটি পূর্ণ সংখ্যার একটি অপরটিকে দিয়ে ভাগ করলে তা অনেকসময় নিঃশেষে বিভাজ্য না হয়ে ভাগশেষ নামক অরেকটি সংখ্যা অবশিষ্ট থেকে যায়। ভাগশেষকে পুনরায় ভাজক দ্বারা ভাগ করলে ভাগফলে পূর্ণ সংখ্যার পরিবর্তে দশমিক পাওয়া যায়। তাই দুটি পূর্ণ সংখ্যার ভাগফল অধিকাংশ ক্ষেত্রে পূর্ণ সংখ্যা হয়না। তবে দুটি পূর্ন সংখ্যাের ভাগফল সব সময়ই মূলদ বাস্তব সংখ্যাগুলির মধ্যই অবস্থান করে।
ভাগের চিহ্ন
সম্পাদনাপ্রায়ই বীজগণিত এবং বিজ্ঞানের বিভিন্ন ক্ষেত্রে ভাজ্য কে একটি অনুভূমিক রেখার উপরে এবং ভাজকে একই রেখার নিচে লিখে প্রকাশ করা হয় এবং এই প্রকাশকে ভাগ্নাংশ বলা হয়ে থাকে।[১] উদাহরণস্বরূপ a কে b দ্বারা ভাগের ক্ষেত্রে লিখা যায়-
এই পদ্ধতি পড়ার সময় বলা হয় a কে b দ্বারা ভাগ অথবা a ভাগ b অথবা b এর a অংশ।œআবার ভাগ প্রকাশের আরেকটি চিহ্ন আছে যেখানে ভাজ্য ও ভাজক কে পরপর লেখে মাঝে একটি '/' চিহ্ন ব্যবহার করা(ইংরেজি উচ্চারণ স্ল্যাশ)। যেমন-
টাইপ করতে সুবিধার জন্য ভাগ প্রকাশের এই পদ্ধতি বিভিন্ন কম্পিউটার প্রোগ্রামিং পরিভাষার ক্ষেত্রে বেশি ব্যবহৃত হয়। তবে কিছু কিছু গাণিতিক সফটওয়্যার এই প্রকাশের বিপরীত ক্রম সমর্থন করে। সেক্ষেত্রে আগে ভাজক পরে ভাজ্য লিখে মাঝে ভাগের চিহ্ন হিসাবে '\'(ইংরেজি উচ্চারণ "ব্যাক স্ল্যাশ") ব্যবহার করা হয়। যেমন-
এই দুই পদ্ধতির মধ্যবর্তী প্রকাশের আরেকটি উপায়-
- a⁄b
উপরের যেকোন একটি উপায় ভাগ প্রকাশের ক্ষেত্রে ব্যবহার করা যায় তবে ভগ্নাংশে প্রকাশের ক্ষেত্রে ভাজ্য ও ভাজক উভয়ই পূর্ণ্য সংখ্যা হতে হয়। ভগ্নাংশের দুটি সংখ্যার একটিকে 'লব' এবং অন্যটিকে 'হর' বলা হয়। ভাগ প্রকাশের দ্বিতীয় পদ্ধতি যা পাটিগণিতে সর্বোচ্চ ব্যবহার হয় তা হল '÷'। যেমন-
আবার কিছু কিছু ক্ষেত্রে a কে b দ্বারা ভাগের ক্ষেত্রে অনুপাত চিহ্নটি ব্যবহৃত হয়। অর্থ্যাৎ a : b ভাগ প্রকাশের এই প্রকাশকে প্রথম ব্যবহার করেন William Oughtred তার 'ক্লেভিজ ম্যাথমেটিকা' বইয়ে যা ১৬৩১ সালে প্রকাশিত হয় পরবর্তীতে গ্রডফ্রিড উইলিয়াম লেবনিটজ এই পদ্ধতিকে জনপ্রিয় করে তোলেন[২]
আবার কিছু কিছু ভাষায় a কে b দ্বারা ভাগ প্রকাশের জন্য অথবা চিহ্ন ব্যবহার করা হয়। ভাগ প্রকাশের এই উপায় সর্বপ্রথম মাইকেল স্টিফ ১৫৪৪ সালে তার এরিথমেটিকা ইন্টিগ্রা নামক বইয়ে প্রথম প্রকাশ করেন।[২]
সরল আকারে লিখার নিয়ম
সম্পাদনাভাগকে সরল আকারে প্রকাশের সঠিক উপায়
ভাগকে সরল আকারে প্রকাশের ভুল উপায়-
ইউক্লিডীয় ভাগ
সম্পাদনাইউক্লিডীয় ভাগ হল ভাগের পাটিগাণিতিক একত্রীকরণ যা অনেকটা পূর্ণ সংখ্যার ভাগের মতই। এখানে ভাজ্য এবং ভাজক যারা উভয়ই পূর্ণ সংখ্যা এবং হলে ভাগফলও সব সময় একটি পূর্ণ সংখ্যা। যেমন লেখা যায়–
পূর্ণ সংখ্যার ভাগ
সম্পাদনাপূর্ণ সংখ্যার ভাগের ক্ষেত্রে সব সময় পূর্ণ সংখ্যা পাওয়া যায় না। ভাগফল পূর্ণ সংখ্যা হবে যদি কেবল ভাজ্য ভাজকের পূর্ণ সাংখিক গুণিতক হয়। যেমন: ১২ কে ৩ দ্বারা ভাগ করলে ৪ পাওয়া যায় (অর্থাৎ, ১২ ÷ ৩ = ৪ অথবা +১২/৩ = ৪) কারণ, ১২ = ৩ × ৪ (যেহেতু, ভাজক = ভাজ্য × ভাগফল + ভগশেষ)। কিন্তু ২৬ কে ১১ দ্বারা ভাগ (+২৬/১১) করলে পূর্ণ সংখ্যা পাওয়া যাবে না, কারণ ২৬; ১১ এর গুণিতক নয়। সেক্ষেত্রে—
- ২৬ কে ১১ দ্বারা ভাগ করলে দশমিক সংখ্যা পাওয়া যাবে।
- কাছাকাছি একটি দশমিক সংখ্যা ভাগফল হতে পারে +২৬/১১ ≈ ২.৩৬ অথবা +২৬/১১ ≈ ২+৩৬/১০০ ।
- ২৬ কে ১১ দ্বারা ভাগ করলে অবশ্যই মূলদ সংখ্যা পাওয়া যাবে +২৬/১১। কিন্তু অধিকাংশ ক্ষেত্রে ভগ্নাংশকে সরলীকরণ করা যায় যেমন ৫২ কে ২২ দ্বারা ভাগ করে লেখা যায় +২৬/১১ এটি সাধারণত লব এবং হরকে তাদের গ.সা.গু দ্বারা ভাগ করে সরলীকরণ (+৫২/২২ = +৫২ ÷ ২/২২ ÷ ২ = +২৬/১১) করা হয়েছে।
শূণ্য দ্বারা ভাগ
সম্পাদনাযেকোনো সংখ্যাকে শূণ্য (০) দ্বারা ভাগ করলে ভাগফল অসঙ্গায়িত হয় অর্থাৎ, +যেকোনো সংখ্যা (যেমন: –৩, –২, –১, ১, ২, ৩)/০ = অসংঙ্গায়িত। কারণ, শূণ্যকে কোনো সংখ্যার গুণিতক রূপে প্রকাশ করা যায় না। যেকোনো সসীম সংখ্যাকে শূণ্য দিয়ে গুণ করলে গুণফল শূণ্য (০) পাওয়া যায়।
জটিল সংখ্যার ভাগ
সম্পাদনাদুটি জটিল সংখ্যাকে ভাগ করলে সব সময়ই অরেকটি জটিল সংখ্যা পাওয়া যায়। যেমন-
এখানে p, q, r, s চারটিই বাস্তব সংখ্যা এবং r ও s শূণ্য নয়।
জটিল সংখ্যার ভাগফলকে পোলার আকারেও প্রকাশ করা যায়।যেমন-
এখানে p, q, r, s বাস্তব সংখ্যা এবং r এর মান শুন্য নয়।
ম্যাট্রিক্সের ভাগ
সম্পাদনাদুটি ম্যাট্রিক্সের ভাগকে প্রকাশ করা হয়- A / B = AB−1, যেখানে B−1; B ম্যাট্রিক্সের বিপরীত ম্যাট্রিক্স প্রকাশ করে। এটাকে সাধারনত দ্ব্যর্থতা নিরসনের জন্য AB−1 রূপে প্রকাশ করা হয়।