অবিচ্ছিন্ন ফাংশন
গণিতে অবিচ্ছিন্ন ফাংশন হচ্ছে এমন ফাংশন বা অপেক্ষক যাতে কোন বিচ্ছিন্নতা নেই,[১] অর্থাৎ যার মান হূঁট করে পাল্টে যায় না।

সংজ্ঞা
সম্পাদনাবাস্তব ফাংশনের জন্য অবিচ্ছিন্নতা
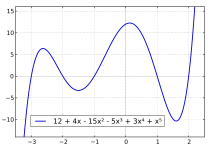
সম্পাদনাবাস্তব ফাংশনের ক্ষেত্রে কল্পনা করা যেতে পারে যে, একটি অবিচ্ছিন্ন ফাংশনের গ্রাফ কলম না তুলেই আঁকা যাবে - এজন্যই একে "অবিচ্ছিন্ন" আখ্যা দেয়া হচ্ছে।
বেশ কয়েক ভাবে বাস্তব অবিচ্ছিন্ন ফাংশনের গাণিতিকভাবে দৃঢ় সংজ্ঞা দেয়া যেতে পারে।
ফাংশনের লিমিট ব্যবহার করে সংজ্ঞা
সম্পাদনাএকটি ফাংশন এর ডোমেইনের একটি বিন্দু -তে অবিছিন্ন হবে যদি ঐ বিন্দুতে -এর লিমিটের অস্তিত্ত্ব থাকে, আর সে লিমিট f-এর ঐ বিন্দুতে যে মান তার সমান হয়। অর্থাৎ সংজ্ঞায়িত হতে হবে ও সত্যি হতে হবে। অন্যথায় উক্ত বিন্দুতে বিচ্ছিন্ন হবে।
একটি ফাংশন যদি এর ডোমেইনের সকল বিন্দুতে অবিচ্ছিন্ন হয়, অর্থাৎ কোথাও বিচ্ছিন্ন না হয়, তাহলে -কে বলা হবে অবিচ্ছিন্ন ফাংশন।
টপোলজিতে অবিচ্ছিন্ন ফাংশন
সম্পাদনাদুটি টপোলজিকাল স্পেস ও এর মধ্যে একটি ফাংশন বিবেচনা করা যাক।
এখানে একটি অবিচ্ছিন্ন ফাংশন হবে যদি স্পেসটির প্রতিটি খোলা সেট এর জন্য
স্পেসটির একটি খোলা সেট হয়।
তথ্যসূত্র
সম্পাদনা- ↑ "Continuous Function - Definition, Examples | Continuity"। Cuemath (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২৪-০২-০৫।